贝叶斯统计/pymc 学习笔记(二)
Doing Bayesian Data Analysis 后面花了 8 章书讲解了如何用贝叶斯统计实现各种分析和预测任务,可见贝叶斯定理的应用有多广泛。今天读完了 Metric Predictor 的部分并且用 pymc 跑了一遍,在这里回顾一下学到了多少内容。这是我第一次读,而且我也不是统计专业的,有很多没有明白的地方就跳过了,可能笔记里有很多写得不对的地方,等以后把不懂的地方弄明白了再回来检查。
所谓的 Metric Predictor,就是可以比较大小的数值数据,例如身高,体重,成绩等。相关的统计任务有,对比两组数据是否属于同一分布,线性回归等。
注:文里的代码用的是 python3。
T-test
对比两组数据是否属于同一分布,传统统计学的方法是 T 测试,计算 t 值,p 值还有 F 值。贝叶斯统计最初的应用就是估计样本的分布,自然也适用于样本的对比。它的优势在于,我们不需要假定样本是正态分布,而可以使用可能更符合现实的 t 分布。当然用模拟的方法去求值效率上肯定没有直接解方程好了。
pymc 例子:
# 生成两组数据,这里设置两个不同的分布 from scipy import stats mu1, std1 = 5, 5 group1 = stats.norm.rvs(loc=mu1, scale=std1, size=100) mu2, std2 = 10, 3 group2 = stats.norm.rvs(loc=mu2, scale=std2, size=100)
然后定义测试模型,均值的先验定义为正态分布,方差定义为均匀分布:
# model with pm.Model() as ttest: mu1e = pm.Normal('mu1', mu=group1.mean(), sd=.1) std1e = pm.Uniform('std1', lower=0, upper=10) g1 = pm.Normal('group1', mu=mu1e, sd=std1e, observed=group1) mu2e = pm.Normal('mu2', mu=group2.mean(), sd=.1) std2e = pm.Uniform('std2', lower=0, upper=10) g2 = pm.Normal('group2', mu=mu2e, sd=std2e, observed=group2) # 需要对比的部分,均值和标准差 mean_dif = pm.Deterministic('Mean dif', mu1e-mu2e) std_dif = pm.Deterministic('Std dif', std1e-std2e)
MCMC,登场~
with ttest: start = pm.find_MAP() step = pm.Metropolis() # Metropolis 方法在书中有很生动的描述 trace_ttest = pm.sample(10000, step, start, progressbar=False)
Sampling……Done!
pm.traceplot(trace_ttest[2000::50], vars=['Mean dif', 'Std dif']) plt.tight_layout()
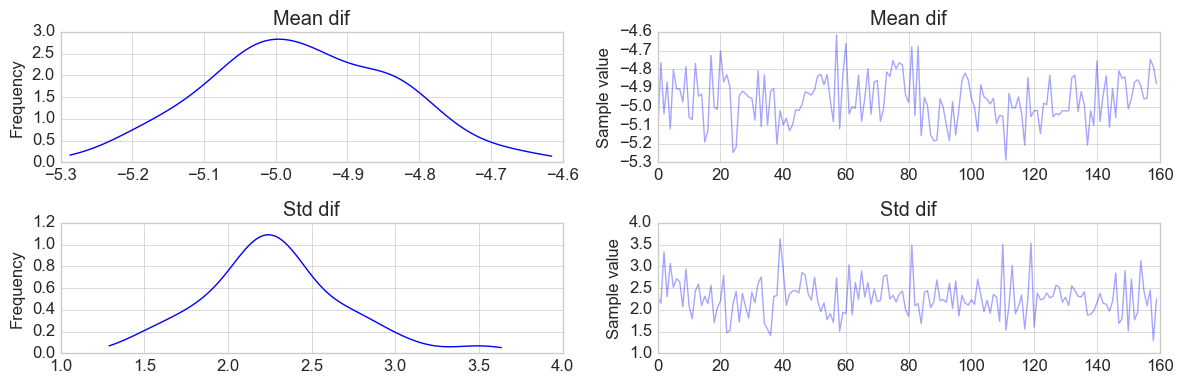
线性回归,一个自变量
处理线性回归问题,通常指定因变量 Y 属于一个正态分布:
\(Y \sim N(\mu, \sigma)\) , 其中 \(\mu = \alpha + \beta X\)
由于现实问题经常会有 outliner 出现,指定 Y 属于 t-分布会产生更加好的结果。
例子:
# Data x = np.linspace(0, 20, 20) a, b = 5, 3 # 需要估计的参数 y = b * x + a + stats.t.rvs(df=1, scale=3, size=np.size(x)) plt.plot(x, y, '.') plt.xlim((-10, 30)) plt.ylim((-10, 80))
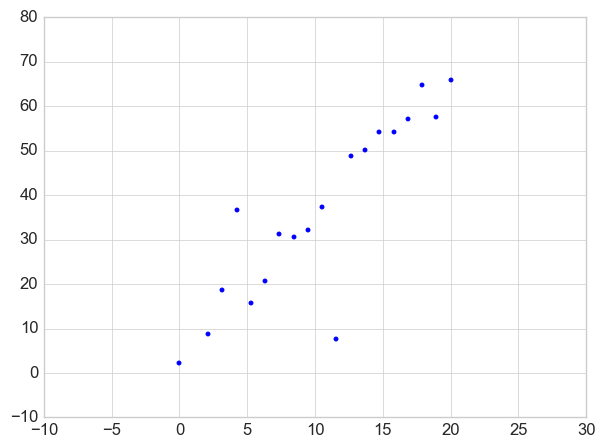
定义模型,用 T 分布来做 Y 的分布,这时,自由度 nu 的先验为指数分布,标准差为均匀分布, alpha 和 beta 为正态分布。如果对变量进行标准化,即使变量变为 0, 方差为 1,那么 alpha 和 beta 的先验均值为 0,但现在这个简单模型,可以从上图看到大概的值。
with pm.Model() as linreg: alpha = pm.Normal('alpha', mu=7, sd=2) beta = pm.Normal('beta', mu=2, sd=2) mu = beta * x + alpha nuMinusOne = pm.Exponential('nu', lam=1) nu = nuMinusOne + 1 lam = pm.Uniform('lam', 0, 10) my = pm.T('Y', nu=nu, mu=mu, lam=lam, observed=y)
继续 MCMC,这次我们用 NUTS sampling,据说在变量数很多的时候能够大大改善效率。在这里是杀鸡用牛刀了。
with linreg: start = pm.find_MAP() step = pm.NUTS(scaling=start) trace_linreg = pm.sample(10000, step, start=start, progressbar=False)
看看结果,注意 a 和 b 的实际值为 5 和 3
pm.summary(trace_linreg[2000::100], vars=['alpha', 'beta'])
alpha: Mean SD MC Error 95% HPD interval ------------------------------------------------------------------- 5.320 1.870 nan [2.114, 9.089] Posterior quantiles: 2.5 25 50 75 97.5 |--------------|==============|==============|--------------| 2.319 4.181 4.991 6.765 9.403 beta: Mean SD MC Error 95% HPD interval ------------------------------------------------------------------- 3.116 0.149 nan [2.852, 3.427] Posterior quantiles: 2.5 25 50 75 97.5 |--------------|==============|==============|--------------| 2.852 3.027 3.117 3.218 3.427
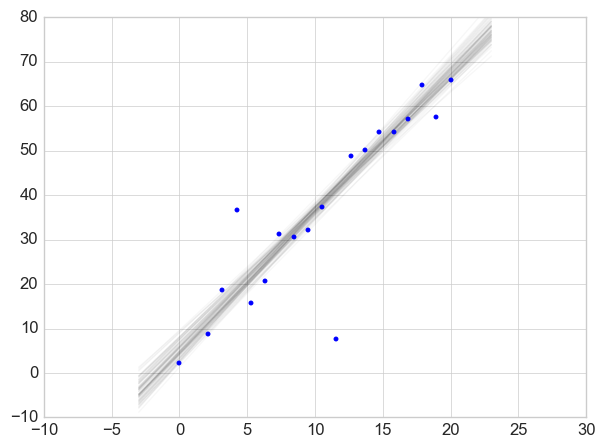
用图片展示,颜色越深,代表确定性越高。
a_p = trace_linreg[2000::100]['alpha'] b_p = trace_linreg[2000::100]['beta'] x_p = np.linspace(-3, 23) for i in range(len(a_p)): y_p = b_p[i] * x_p + a_p[i] plt.plot(x_p, y_p, 'k', alpha=.03) plt.plot(x, y, '.') plt.xlim((-10, 30)) plt.ylim((-10, 80))
线性回归,多个自变量
多个自变量和一个自变量的模型基本是一致的,只是要给每个自变量的 beta 值指定先验。这时候用变量标准化可以简化模型。
下面的例子的数据用的是 Andrew Ng 的 machine learning 课程里面的习题数据。
x = data['X'].flatten() y = data['y'].flatten() plt.plot(x, y, 'bx') plt.xlim((-60, 50)) plt.ylim((-10, 50))
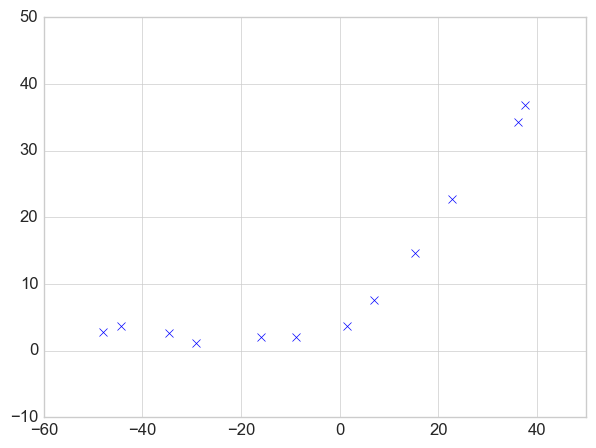
因为变量只有一个,而且这个图看着也像是多项式函数的图像,所以先弄一些多项式 feature,然后再定义我们的模型。
# get polynomial features x_mat = np.c_[x, (x**2), (x**3)] # standarize the feature x_mu = x_mat.mean(axis=0) x_std = x_mat.std(axis=0) x_mat[:, 0] = (x_mat[:, 0] - x_mu[0]) / x_std[0] x_mat[:, 1] = (x_mat[:, 1] - x_mu[1]) / x_std[1] x_mat[:, 2] = (x_mat[:, 2] - x_mu[2]) / x_std[2] # also standardize the target y_mu = y.mean() y_std = y.std() y_mat = (y - y_mu) / y_std # Model with pm.Model() as polymol: b0 = pm.Normal('b0', sd=50) b1 = pm.Normal('b1', sd=50, shape=(3,)) zsigma = pm.Uniform('zsigma', 1.0E-5 , 1.0E-1) nuMinusOne = pm.Exponential('nu-1', lam=1/29) nu = nuMinusOne + 1 mu = b0 + pm.dot(b1, x_mat.T) obv = pm.T('observed', mu=mu, nu=nu, lam=1/(zsigma**2), observed=y_mat) beta0_ = (y_std * b0) + y_mu - y_std * pm.sum(b1 * x_mu / x_std, axis=0) beta1_ = y_std * (b1 / x_std) beta0 = pm.Deterministic('beta0', beta0_) beta1 = pm.Deterministic('beta1', beta1_)
继续 MCMC,这个例子稍微复杂一点。其实全部用 NUTS 或者 Metropolis 也是可以的。
with polymol: start = pm.find_MAP() # Find starting value by optimization step1 = pm.NUTS([b1]) step2 = pm.Metropolis([b0, zsigma, nu]) trace = pm.sample(10000, [step1, step2], start, progressbar=False)
看看结果如何。
pm.summary(trace[2000::50], vars=['beta0', 'beta1'])
beta0: Mean SD MC Error 95% HPD interval ------------------------------------------------------------------- 5.238 0.602 0.056 [4.122, 6.366] Posterior quantiles: 2.5 25 50 75 97.5 |--------------|==============|==============|--------------| 4.134 4.864 5.226 5.688 6.456 beta1: Mean SD MC Error 95% HPD interval ------------------------------------------------------------------- 0.384 0.038 0.004 [0.308, 0.456] 0.010 0.001 0.000 [0.009, 0.011] 0.000 0.000 0.000 [0.000, 0.000] Posterior quantiles: 2.5 25 50 75 97.5 |--------------|==============|==============|--------------| 0.308 0.361 0.383 0.410 0.456 0.009 0.010 0.010 0.011 0.011 0.000 0.000 0.000 0.000 0.000
下图仍然是颜色越深的线,确定性越高。
beta0 = trace['beta0'][2000::50] beta1 = trace['beta1'][2000::50] plt.plot(x, y, 'x') x_t = np.linspace(-55, 55) x_pred = np.c_[x_t, (x_t**2), (x_t**3)] for i in range(len(beta0)): y_p = np.dot(beta1[i], x_pred.T) + beta0[i] plt.plot(x_pred[:, 0], y_p, 'k-', alpha=.02)
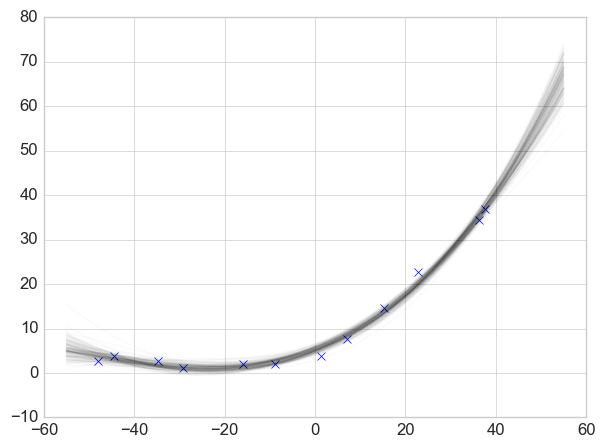
可以看到,三次项的系数基本等于 0,说明这一项对预测几乎没有作用。这一点可以帮助我们选择哪些变量。另一个方法是,给每个变量乘一个参数,这个参数符合博努利分布,如果最后结果这个参数的 p 小于一个阀值就可以认为对应的变量影响力太小可以忽略。
以上。